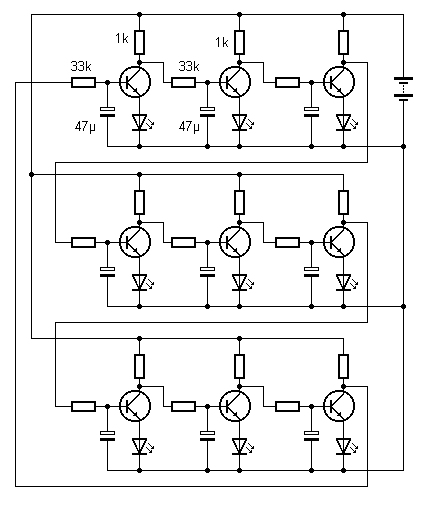
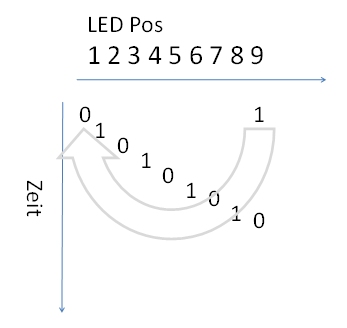
Analoges Lauflicht mit neun LEDs

Mit drei LEDs hatte ich die Schaltung ja schon gebaut (siehe Elektronik-Kalender 08, Dreiphasen-Blinker). Aber im Prinzip müsste die Schaltung mit jeder beliebigen ungeraden Zahl LEDs funktionieren. Also ein Test mit neun LEDs. Alles wurde mit Bauteilen aus der Bastelkiste auf einen Kaffeedeckel gelötet. Neun Stufen sind günstig, weil man freihändig ohne Winkelmesser die Verteilung einigermaßen hinbekommt. Übrigens, die Ähnlichkeit mit einem Ringoszillator ist kein Zufall. Nur gibt es hier noch Verzögerungsglieder zwischen den Stufen.

Kommt dem Ingenieur die Aufgabe lösbar vor,
hebt das die Stimmung im Labor.
(Dietrich Drahtlos)

Gebaut und ausprobiert, die Schaltung hat auf Anhieb funktioniert. Aber wie sie funktioniert, das hat mich überrascht. Wenn man nur zwei LEDs betrachtet, sieht es aus wie ein Wechselblinker. Im wesentlichen sieht man immer eine leuchtende LED neben einer dunklen LED. Aber im schnellen Kreislauf wechseln die Zustände. Ich musste etwas länger nachdenken, bis ich verstanden habe, wie das abläuft. Jede Stufe ist ein Inverter. Im Prinzip wäre dies ein stabiler Zustand:

010101010

Aber weil die letzte Stufe auf die erste zurückgekoppelt ist, passt da etwas nicht. Die linke Stufe kippt also mit einer kleinen Verzögerung um, was dann den nächsten Wechsel auslöst usw. Im Endeffekt läuft eine Störung im Kreis herum:

110101010
111010101
011101010
101110101
010111010
101011101
010101110
101010111
100101011

Das sieht zwar ziemlich digital aus, aber tatsächlich gibt es weiche Übergänge. Und wenn man länger hinschaut, scheint ein Licht im Gegenuhrzeigersinn im Kreis herum zu sausen. Auf jeden Fall ist das Ergebnis völlig anders als bei drei Stufen. Eigentlich wüsste ich jetzt gern, wie es mit fünf oder sieben Stufen funktioniert. Wenn es mal jemand ausprobiert, würde ich mich über eine Nachricht freuen.

http://www.youtube.com/user/bkelektronik

Alan hat die Schaltung mit fünf und mit sieben LEDs gebaut: http://www.youtube.com/watch?v=D02jP30TP4I
Experimente mit 39 Stufen: http://www.youtube.com/user/vk2zay#p/u/2/mVCW2A0C68A
DieroteFahne hat eine Version mit 61 roten und grünen LEDs gebaut: www.youtube.com/user/DieroteFahne#p/u/0/wG2PpncOY2g

Überlegungen von Udo Wollmann
Die Zeile 010101010 stimmt nur scheinbar, und führt zu dem Widerspruch, dass der rechte Inverter mit 0 zum Zustand des ganz linken Inverters ebenfalls mit 0 führt. In Wirklichkeit ist es doch so, das die kleinen Phasenverschiebungen im Summe dazu führen, das beim Erscheinen der ganz linken Null ganz rechts schon wieder eine 1 steht (und damit ist es wieder ein Inverter). Oder anders ausgedrückt, die Darstellung der 01-Folge in einer Zeile impliziert das gleichzeitige Auftauchen der 0 an beiden Enden, und dann würde der Ringosz. tatsächlich nicht schwingen, sondern wäre eher ein "Ringspeicher". Auch kann ich den Zustand ..01110... ( also drei benachbarte LED im gleichen oder fast gleichen Zustand) im Video nicht erkennen. Hier habe ich die Zeile versucht mit Zeitverschiebung darzustellen, damit schließt sich dann der Kreis im wahrsten Sinne des Wortes. Natürlich kann auch bei mir noch ein Denkfehler sein, selbst sehr einfache Dinge können eine sehr komplexe innere Natur haben.

Nachtrag: Mir ist auch aufgefallen, dass der Film eigentlich was anderes zeigt. Es kommt noch dazu, dass das tatsächliche Ergebnis stark von der Betriebsspannung abhängt. Tatsächlich läuft ja eine Art Sinuswelle durch die Schaltung. Ab welcher Schwelle eine LED an ist, hängt u.a. von der Versorgungsspannung ab. Je höher sie ist, desto mehr LEDs scheinen gleichzeitig an zu sein. Weil ich relativ schlappe LEDs verwendet habe, hatte ich die Spannung für den Film auf 24 V erhöht. An der unteren Grenze bei ca. 4 V sieht es eher so aus, als würde eine dunkle Welle durch den Kreis laufen. Alan's Film zeigt, dass bei fünf oder sieben LEDs da gleiche passiert. Wenn man den Film zwischendurch mal stoppt, kann man den Eindruck haben, dass immer vier LEDs gleichzeitig leuchten, aber nicht gleich hell. In der Tat, die Sache ist komplizierter als man meinen könnte.

Physikalische Erklärung Hans Martin Sauer

Um die Lichteffekte in Ihrem Ringoszillator verstehen zu können, habe ich mir erlaubt, die normale digitale Notation aus 0 und 1 durch "-1" und "+1" zu ersetzen. Beispielsweise entspricht

010101110

der Zahlenfolge

-1,+1,-1, +1,-1,+1,+1,+1,-1

Das hat den Vorteil, dass man damit die invertierenden Eigenschaften jeder der 9 Inverterstufen einfach als Gleichung aufschreiben kann. Die Spannung am Eingang der (n+1)-ten Inverterstufe ergibt sich aus der Spannung am Eingang der n-ten Stufe (gegen einen passend definierten Spannungs-Mittelwert) zu

U(n+1) = - U(n)

Das stimmt jedenfalls im statischen Zustand. Wenn jedoch eine zeitliche Änderung der Spannungen an den Invertereingängen stattfindet, ist das nicht mehr ganz so, und man muss zur Korrektur einen Phasenfaktor dazuschreiben. Es scheint mir plausibel anzunehmen, dass diese Phasenverschiebung zur dominierenden Frequenz f der Spannungsänderung und zur Zeitkonstante T = R C der einzelnen RC-Glieder proportional ist:

U(n+1) = - exp(2 * pi * j * f * T) U(n)

bzw.

U(n+2) = (-1) (-1) exp(2 * 2 * pi * j * f * T) U(n)

U(n+3) = (-1) (-1) (-1) exp(2 * 3 * pi * j * f * T) U(n)

... usw.,

wobei j die imaginäre Einheit (j * j = -1) ist.

Jetzt kommt der eigentliche Trick: Nun muss nämlich, wenn die 9. Stufe (oder allgemeiner die N-te Stufe, wobei N ungerade sein möge) wieder zurück auf den Eingang der ersten Stufe gekoppelt wird, folgendes gelten:

U(1) = (-1)^N exp(2 * N * pi * j * f * T) U(1)

Klar, U(9+1) = U(1) hat zu jedem Zeitpunkt eindeutigen Wert. Die Notation (-1)^N bedeutet hier "-1 hoch N". Nun ist ferner (-1)^N = -1, da N ungerade ist. Also muss die Zahl im Exponenten der e-Funktion ein ungeradzahlig Vielfaches von j*pi sein, oder nach Fortlassen von j und pi:

2 N f T = 2 k - 1

wobei k = 1,2,3,... beliebige positive ganzzahlige Werte annehmen darf. Zu jedem dieser k-Werte gibt es also eine Lösung des Problems bzw. ein mögliches Leuchtmuster, wobei k gleichzeitig die Anzahl der Helligkeitsmaxima angibt, die in Ringoszillator unterwegs sind, und

f = f(k) = (2 k - 1) / (2 N T)

die Umlauffrequenz des jeweiligen Musters angibt. Es ist klar, dass im vorliegenden Fall die Lösungen mit 2 k -1 > N = 9 nicht mehr relevant sind, da ja nur 9 LEDs und damit maximal 4 Maxima existieren können.

Welche von diesen Leuchtmustern nun tatsächlich entsteht, hängt wohl von den Nichtlinearitäten der Inverterstufen ab. In Wirklichkeit wird man eine Überlagerung verschiedener Muster beobachten. Wäre die Verstärkung vollkommen linear, dann könnte man die einzelnen Muster nach belieben überlagern. Mich wundert daher auch nicht, dass das Leuchtmuster von der Betriebsspannung abhängt, weil damit man dadurch ja auch die Arbeitspunkte der Transistoren, bzw. die Nichtlinearität der Signalverstärkung beeinflusst. Vielleicht können Sie ja mal versuchen, Ihren Ringoszillator mit einer dieser Frequenzen f(k) zu "triggern". Es müsste dann tatsächlich das betreffende Leuchtmuster über die anderen die Oberhand gewinnen.

Übrigens ist dieses LED-Lauflicht ein wunderbares Demonstrations-Experiment für die Entstehung von Bandstrukturen in Metallen und Halbleitern, wenn man eine Analogie zwischen den Zuständen "An" und "Aus" der LEDs mit den atomaren Elektronenzuständen "unbesetzt" und "besetzt" in einem (stark vereinfachten) Halbleiteratom benutzt. Wenn man die Inverterstufen nicht miteinander verbindet, hat jede abhängig von den Anfangsbedingungen nur zwei mögliche Zustände: "-1" (Elektronen-Zustand im Atom unbesetzt), und "+1" (Elektronenzustand besetzt). Wenn man die Inverter jedoch miteinander koppelt, dann entstehen neue, dynamische Zustände (hier durch die Zahl k gekennzeichnet). Hierbei ist keinem Inverter eindeutig ein "-1" oder "+1" zugeordnet, bzw. keinem der aneinader gebundenen Atome ein festes Elektron. In den neu entstandenen Zuständen bewegen sich die Leuchtmuster (bzw. Elektronen) mit verschiedenen Frequenzen (bzw. Energien) an der Kette der Inverter (bzw. Atome) entlang.

Zusatzexperiment: Zum Test, ob auch höhere Frequenzen entstehen können, habe ich einzelne Basen kurzgeschlossen und dann wieder frei gelassen. Dabei entstehen komplizierte Muster mit höheren Frequenzanteilen. Aber nach kurzer Zeit geht zumindest für den frei laufenden Oszillator alles wieder ins Grundmuster über. Der Grund könnte sein, dass die Dämpfung der Tiefpassfilter bei der kleinsten Frequenz am geringsten ist.

Röhren-Lauflicht von Hans Martin Sauer

Nicht nur mit Transistoren, sondern auch mit Röhren lässt sich ein gut funktionierendes Lauflicht realisieren. Ich habe dazu eine EL 95 bzw. ELL 80, die in der beigefügten Schaltung im leitenden Zustand an der Anode kaum mehr als 10 V Restspannung haben. Sicherlich geht es auch mit anderen Pentoden, sofern sie genügend Anodenstrom für die Glühbirnen liefern können. Passende Glühbirnen für 130 V, 20 mA habe ich den Kontroll-Leuchten eines ausgemusterten Maschinenschaltpults entnehmen können.

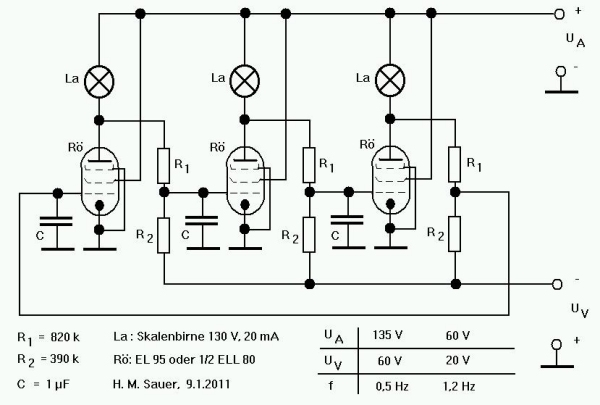
Habe eine 3-fach- und eine 5-fach-Version des Lauflichts auf dem Steckbrett aufgebaut. Lief beides auf Anhieb, wobei bei der 3-fach-Version immer nur eine Birne brennt und zwei aus sind, und bei der 5-fach-Version zwei Birnen an jeweils gegenüberliegenden Positionen des Ringoszillators an sind. Die An/Aus-Umschaltung ist recht schnell, quasi digital. Den Schaltplan für das 3-fach-Lauflicht habe ich beigefügt, der für's 5-fach Licht hat einfach zwei Röhrenstufen mehr.

3-stufiges Lauflicht (mit 1 x EL 95 und 1 x ELL 80): www.youtube.com/watch?v=zlRCR2-r758

5-stufiges Lauflicht (mit 1 x EL 95 und 2 x ELL 80): www.youtube.com/watch?v=CywMX1qlIIA

Sieht irgendwie nach Adventskranz bzw. Weihnachten aus. Meine Frau war vollauf begeistert. Zum nächsten Weihnachtsfest will sie ein mindestens 7-stufiges Licht als Wohnzimmerdeko. Habe ich mangels passender Röhren bisher noch nicht ausprobieren können.

Das Röhren-Lauflicht benötigt neben der Anodenspannung noch eine weitere, negative Spannungsquelle, die jedoch nur Bruchteile eines mA liefern muss. Ansonsten erreichen die Röhren keinen sperrenden Zustand. Das Lauflicht funktioniert auch mit nur 60 Volt Betriebsspannung einwandfrei, wobei natürlich Glühbirnchen mit entsprechender Betriebsspannung besser geeignet wären als die, die ich verwendet habe.

Home Labor Röhren HF Logbuch Bastelecke